|
Éléments |
Isotope(s) |
Constitution |
|
|
|
|
|
Hydrogène |
Hydrogène (H) |
1 p (Prépondérant) |
|
|
Deutérium (D) |
1 p et 1n |
|
|
Tritium (T) |
1 p et 2n |
|
|
|
|
|
Helium (He) |
Hélium 4 (4He) |
2 p et 2n
(Prépondérant) |
|
|
Hélium 3 (3He) |
2 p et 1n |
|
|
|
|
|
Lithium (Li) |
Lithium 7 (7Li) |
3 p et 4n
(Prépondérant) |
|
|
Lithium 6 (6Li) |
3 p et 3n |
|
D+T = 4He
(3,52 MeV) + n (14,1 MeV) |
I1a |
|
|
|
|
D+D = T (1,01 MeV) + p
(3,02 MeV) |
I2a |
|
|
|
|
D+D = 3He
(0,82 MeV) + n (2,45 MeV) |
I3a |
|
|
|
|
D+3He =
4He (3,07 MeV) + p (14,07 MeV) |
I4a |
|
|
|
|
7Li +n =
4He + T + n (-2,47 MeV) |
I1b |
|
|
|
|
6Li +n =
4He (2,05 MeV) + T (2,73 MeV) |
I2b |
Remarques :
-I2a et I3a se produisent en proportions
égales
-Dans un réacteur on I1a + I2b qui conduisent à
l’équation bilan
D+6Li = 2 4He + Énergie
Considérons la réaction I1a. On pèse les éléments du membre de
gauche (D et T) et de droite (4He et n). Les résultats sont les
suivants :
D et T pèsent 4,992722*mp
4He et n pèsent 4,973974*mp
On a donc une différence de masse dm=0,018747*mp
D’où une énergie libérée de E = dm*c2 = 2,818.10-12 J
= 17,59 MeV
|
L’énergie de
liaison d’un nucléon dans un noyau passe par un maximum pour les noyaux
voisins du fer
Les atomes légers
gagnent en stabilité en fusionnant car ils possèdent (après réaction)
d’un A plus important
Les atomes lourds,
au contraire, augmentent leur stabilité en fissionnant, c'est-à-dire en
diminuant leur A
B: nombre de protons |
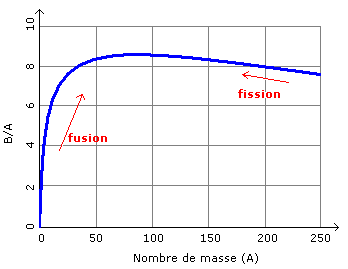 |
Pente
fusion > Pente fission donc la fusion développe plus
d’énergie que la fission.
En effet, pour la fission un élément gagne peu en perdant un neutron BA-1
peu supérieur à BA
A contrario pour la fusion BA << BA+1. Donc la
fusion est plus stabilisatrice que la fission
La fusion des noyaux légers et la fission des noyaux lourds leur permet de
se rapprocher de la zone de stabilité maximale. C’est pourquoi ces réactions
sont exoénergétiques (libèrent de l’énergie)
|